차등 금융 모델의 Δ 추정을 위한 트윈 타워 신경 아키텍처
링크 표
추상적인
-
키워드 및 2. 서문
-
설정
-
고전적인 결과에서 차등 기계 학습으로
4.1 위험 중립 가치 평가 접근 방식
4.2 차등 머신러닝: 손실 함수 구축
-
예: 디지털 옵션
-
기초 선택
6.1 고정기준의 한계
6.2 매개변수 기반: 신경망
-
시뮬레이션-유럽 통화 옵션
7.1 블랙숄즈
7.2 헤징 실험
7.3 최소제곱 몬테카를로 알고리즘
7.4 차등 기계 학습 알고리즘
-
수치 결과
-
결론
-
이해상충 진술 및 참고자료
메모
7 시뮬레이션-유럽 통화 옵션
7.1 블랙숄즈
블랙숄즈 모델을 고려해보세요:
\

\
7.2 헤징 실험
이 실험은 만기 T인 유럽 콜 옵션을 매도하는 것으로 시작됩니다. 파생상품은 기초 자산을 거래하여 헤지됩니다. Δ 헤징 전략이 고려되며, 새로 계산된 Δ 가중치에 따라 기초 포지션으로 구성된 포트폴리오가 매주 재조정됩니다.
\ \
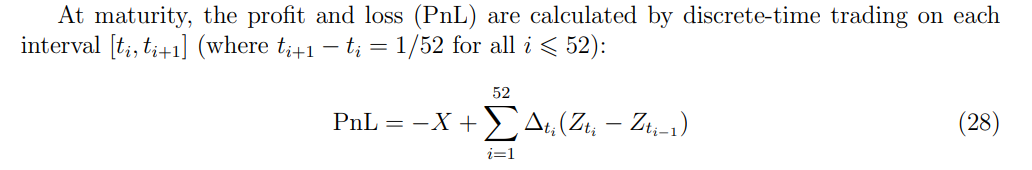
\ \ n 경로에 걸친 Z의 진화 시뮬레이션이 수행되어 n PnL 값이 생성됩니다. 히스토그램은 경로 전체에 걸친 PnL 값의 분포를 시각화하는 데 사용됩니다. 그런 다음 다양한 방법을 이 실험에 적용하고 그 결과를 BlackScholes 사례와 비교합니다.
\ PnL 값은 매도된 유럽 콜 옵션의 프리미엄인 0기간의 포트폴리오 가치를 기준으로 보고됩니다. 상대 헤징 오류는 생성된 히스토그램의 표준 편차로 측정됩니다. 이 측정항목은 Frandsen et al., 2022에서와 같이 다양한 모델의 성능을 평가하는 데 널리 사용됩니다.
\
7.3 최소제곱 몬테카를로 알고리즘
7.3.1 단항 기초
\ \
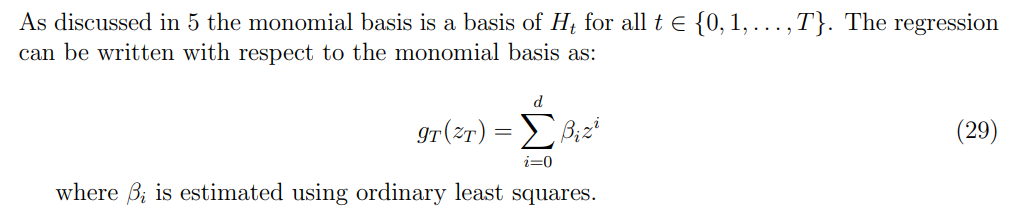
\ \
7.3.2 신경망 기반
\ 또는 회귀는 신경망과 같은 매개변수 기반을 사용하여 수행될 수 있습니다.
\ \

\ \ 신경망의 아키텍처는 중요하며, 명제 5.3과 다양한 응용 분야의 경험적 연구에 의해 뒷받침되는 것처럼 l > 1인 다층 신경망이 선호됩니다. 이 예에서 레이어 차원은 l = 4로 설정되어 설명력을 위해 더욱 미세 조정될 수 있습니다. 역전파 알고리즘은 각 에포크 이후 가중치와 편향을 업데이트하는 데 사용되며, Kingma 및 Ba, 2014에서와 같이 확률적 경사하강법을 통해 내부 매개변수에 대한 손실 함수를 최소화함으로써 달성됩니다.
\
7.4 차등 기계 학습 알고리즘
명제 3.4로부터, 주어진 표본 ((x1, z1)), . . . ,(xn, zn)), 훈련 샘플에 대한 손실 함수는 다음과 같습니다.
\ \
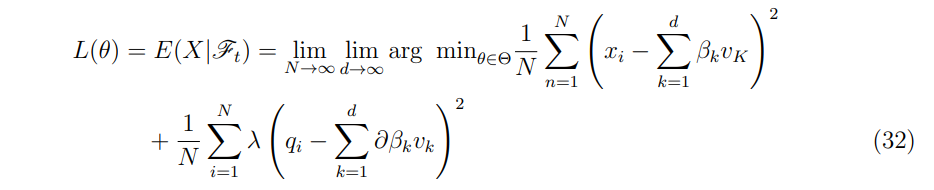
\ \ \ \ \

\ \ 최소 두 개의 서로 다른 경로에 대한 시뮬레이션을 통해 qi를 계산하고 지표 함수를 적용한 후 결과 수량을 평균화하여 Δ 헤징 추정치를 얻습니다. 이 방법은 효율적이고 정확한 헤징 전략을 가능하게 하여 수학 금융 분야에서 귀중한 도구가 됩니다.
\
7.4.1 신경망 기반
\ 이 구현에 대한 모든 세부 사항은 Huge and Savine, 2020에서 확인할 수 있습니다. 방정식 (30)을 살펴보면 첫 번째 부분은 LSMC 사례와 동일한 손실 함수입니다. 그러나 두 번째 부분은 가격과 관련하여 차등 라벨과 전체 신경망 파생 상품 간의 평균 제곱 차이를 구성합니다. 따라서 우리는 피드포워드 신경망의 파생물을 얻어야 합니다. 피드포워드 신경망은 역전파를 통해 효율적으로 차별화됩니다.
\ 그런 다음 피드포워드 방정식을 요약하면 다음과 같습니다.
\ \
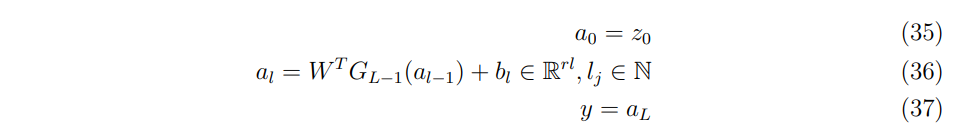
\ \ 입력은 상태이고 예측 변수는 첫 번째 부분에 대한 가격이라는 점을 상기하십시오. 따라서 이러한 차이는 위 선을 역순으로 차별화하여 얻은 예측 위험 민감도입니다.
\ \
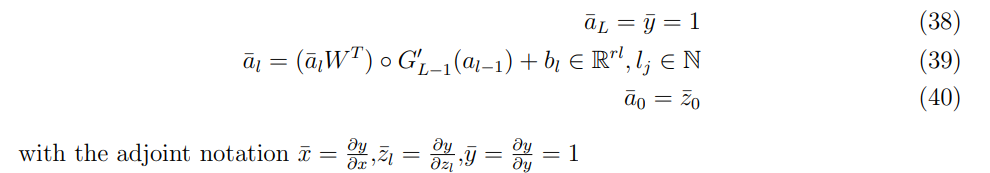
\ \ 그런 다음 구현은 다음 두 단계로 나눌 수 있습니다.
\
-
표준 피드포워드 방정식 (35)-(37)에 대한 신경망은 모든 중간 값을 저장하는 소프트웨어 기능의 사용에 세심한 주의를 기울여 구축되었습니다. 신경망 아키텍처는 섹션 6.2.1에 규정된 다중 계층 구조인 4개의 숨겨진 계층을 포함합니다. 방정식 (38)-(40)을 적용하려면 활성화 함수가 미분 가능해야 하므로 다음 Huge and Savine, 2020에서는 소프트 플러스 함수가 선택되었습니다.
\
-
방정식 (35)-(37)을 Python의 표준 함수로 구현합니다. 이전에 저장된 중간 값은 이 함수의 영역이 될 것입니다.
\
-
트윈 타워라는 단일 기능으로 두 기능을 결합합니다.
\
-
손실 방정식(14)과 관련하여 트윈 타워를 훈련합니다.
\
:::정보
작가:
(1) Pedro Duarte Gomes, 코펜하겐 대학교 수학과.
:::
:::info 이 논문은 arxiv에서 사용 가능 4.0 Deed(Attribution 4.0 International) 라이센스에 의한 CC에 따라.
:::
\














Post Comment