성공 및 안전 테스트의 정확성을 향상시키는 방법
링크 표
초록 및 1 소개
1.1 관련 문헌
-
메트릭 유형 및 가설 및 2.1 유형의 메트릭스
2.2 다양한 유형의 메트릭에 대한 가설
-
우월성 및 비 회비 테스트를 포함한 의사 결정 규칙에 대한 I 형 및 유형 II 오류율
3.1 복합 가설 우월성 및 비 등반 테스트
3.2 UI 및 IU 테스트의 타입 I 및 유형 II 오류율 경계
3.3 성공 및 Guardrail Metrics를 포함한 의사 결정 규칙의 오류율 경계
3.4 비 등반 테스트를위한 전력 보정
-
결정 규칙을 악화 및 품질 메트릭으로 확장합니다
-
몬테 카를로 시뮬레이션 연구
5.1 결과
-
토론과 결론
부록 A : 추가 가정으로 제안 4.1의 효율성 향상
부록 B : 전 세계 허위 및 진정한 긍정적 인 비율의 예
부록 C : 열화의 순차적 테스트에 대한 메모
부록 D : Nyholt의 효율적인 수의 독립 테스트 방법을 사용합니다
승인 및 참고 문헌
부록 A : 추가 가정이있는 제안 4.1의 효율성 향상
성공 지표 및 가드 레일 메트릭에 대해 열등한 테스트 거부 영역이 각각 우수성 또는 비 등반 테스트의 거부 영역과 겹치지 않는 가정을함으로써 효율성을 향상시킬 수 있습니다. 아래 섹션에서, 우리는 악화 테스트가 우수성 및 비 회비 테스트에 대한 유형 I 및 유형 II 오류율에 어떤 영향을 미치는지에 대해 설명합니다. 그런 다음이 정보를 사용하여 제안 4.1을 업데이트합니다.
A.1 우월성 및 악화 테스트를 가진 성공 지표의 유형 I 및 II 형 오류율
추가 악화 테스트를 통해 성공 지표를 테스트 한 결과에 대해 구체적으로하려면 새로운 표기법이 필요합니다. 우리는 단일 성공 지표 와이 메트릭이 운송 결정에 어떻게 기여하는지에 중점을 둡니다. 이제 성공 지표에 대한 두 가지 테스트와 4 개의 가설이 있습니다.
악화 테스트는 여기서 주요 우수성 테스트를 반영하는 열등 성 테스트입니다. 이 두 가지 테스트로 인해 이제이 메트릭에 대한 두 가지 가능한 잘못된 양의 결과가 있습니다 : 잘못된 양성 열등성 테스트와 잘못된 양성 우수성 테스트. 우월성과 열등 성 테스트를 가진 일련의 성공 지표에 대한 운송 결정 측면에서 잘못된 긍정적 위험은 우월성 테스트가 귀무 가설을 거부하는 반면 동시에 열등 성 테스트는 그렇지 않을 확률에 의해 주어집니다. 중요하지 않은 열등 성 테스트의 추가 기준은 우월성 테스트를보다 보수적으로 만들 수 있으며 즉, 배송 결정의 잘못된 긍정적 비율과 실제 긍정적 인 비율을 줄일 수 있습니다. 그러나 악화 테스트의 거부 영역과 우월성 테스트의 거부 영역을 쉽게 제한하여 악화 테스트가 가설에서 우수성 테스트의 거부율에 영향을 줄 수 없도록하기 쉽습니다. Lemma A.1은 이것을 공식화합니다.
Lemma A.1은 동일한 테스트 통계가 우수성 테스트 및 악화 테스트에 사용되는 경우 α_라고 말합니다.
A.2 비 등반 및 악화 테스트를받은 GuardRail 메트릭의 유형 I 및 Type II 오류율
Guardrail Metrics의 경우 성공 메트릭 사례와 유사하게 추론 할 수 있지만, 악화의 거부 영역과 비 등반 테스트 간의 잠재적 중첩으로 인해 추가 뉘앙스가 있습니다. 4 가지 관련 가설이 있습니다
β ≥ α-가 거부 영역이 비 등반 사례에서 겹치지 않는 충분한 추가 기준이라는 사실은 아마도 그래픽으로 가장 쉽게 볼 수 있습니다. 그림 2는 β = α_ 인 영역 간의 관계를 보여줍니다. 그림에서 α_가 증가하면 영역이 고정 된 β에 대해 겹치는 것이 분명합니다. 동시에, β의 감소는 고정 된 α_의 영역이 겹치게한다. α_ ≤ 1 -α+만큼 α+의 값은 오버랩에 영향을 미치지 않습니다. 이는 α+가 변하기 때문에, 비 회비 시험에 전력 1-β가 그에 따라 변화하는 묵시적 NIM이 뒤 따른다.
A.3 발의안 4.1의 업데이트 버전
여기서 우리는 비 겹치는 거부 영역을 시행하여 α 및 β 보정을 약간 향상시킵니다.
증거. 증거는 제안 4.1의 증명과 거의 동일합니다. 이제 우리는 글로벌 널 아래에 있습니다
암시합니다
우리는 α의 수정을 조정하여 해결을 통해 테스트를 덜 보수적으로 만들 수 있습니다.
이는 우리가 α에 따라 수정해야한다는 것을 의미합니다
데이터 생성 프로세스에 대한 가정없이 보수 성을 최소화합니다.
유형 II 오류율의 경우 제안 4.1 증명을 면밀히 따릅니다. 유일한 변화는 그 것입니다
A.4 추가 대략적인 개선
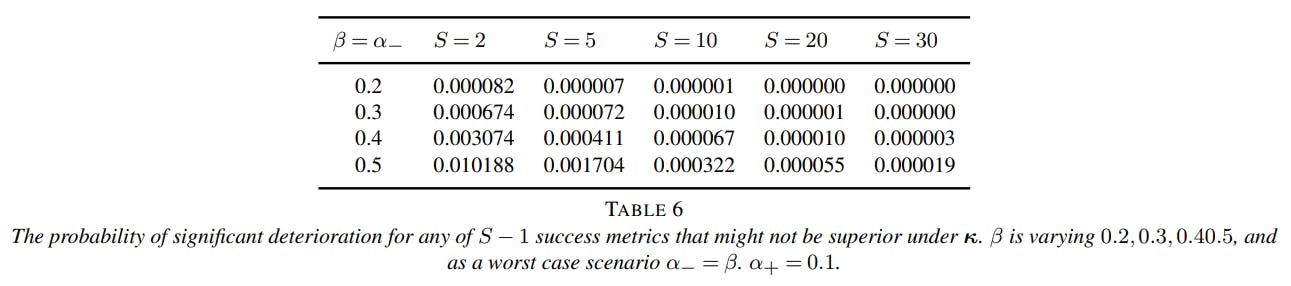
업데이트 된 제안의 β 보정은 매우 극단적 인 최악의 시나리오에서 타입 II 오류율과 결속됩니다. 이는 대안 하에서 적어도 하나의 성공 지표가 개선되었다는 점을 감안할 때 나머지 성공 메트릭 중 하나가 상당히 열등 할 확률이 매우 낮기 때문입니다. 실제로, 확률은 너무 낮아서 일반적으로 무시할 수 있습니다. 우리는 이것을 비고 A.1에서 공식화합니다.
그 말이 이전 증거에서 즉시 뒤 따릅니다.
저자 :
(1) Mårten Schultzberg, 실험 플랫폼 팀, Spotify, 스톡홀름, 스웨덴;
(2) Sebastian Ankargren, 실험 플랫폼 팀, Spotify, 스톡홀름, 스웨덴;
(3) 스웨덴 스톡홀름, Spotify, 실험 플랫폼 팀의 Mattias Fromberg.










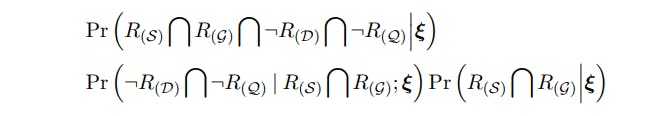

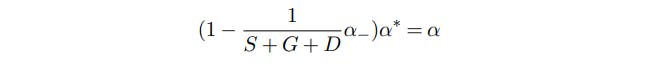





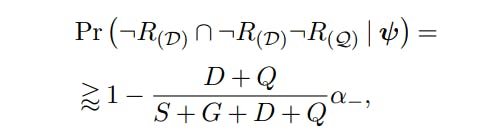













Post Comment