새로운 연구에 따르면 고전적인 이기적인 광업은 구식이라는 것을 보여줍니다

링크 표

초록 및 1. 소개

1.1 관련 작업

2. 예비

   2.1 시스템 모델

   2.2 이기적인 광업 목표

   2.3 Markov 결정 과정

3. 이기적인 광업 공격

   3.1 개요

   3.2 공식 모델

   3.3 공식 분석

   3.4 주요 기능 및 제한

4. 실험적 평가

5. 결론, 인정 및 참고 문헌

A. NAS 채굴 목표

B. 효율적인 증거 시스템

C. 정리 증명 3.1

4 실험 평가

우리는 섹션 3에 제시된 MDP 모델과 공식 분석 절차를 구현하고 다음 연구 질문 (RQ)에 대한 실험적 평가를 수행합니다.

RQ1 우리의 이기적인 광업 전략이 달성하는 예상 상대 수익은 얼마입니까? POW 블록 체인에 대한 고전적인 이기적인 광업 공격의 직접 확장과 비교되는 방법 [11] 아니면 정직하게 채굴하기 위해?

RQ2 시스템 모델 매개 변수의 다양한 값이 이기적인 광업 공격이 달성 할 수있는 예상 상대 수익에 어떤 영향을 미칩니 까? 시스템 모델 매개 변수에는 적의 상대 자원이 포함됩니다. [0, 1] 그리고 스위칭 확률 ing ∈ [0, 1].

기준. 이 RQ에 응답하기 위해, 우리는 이기적인 광업 공격을 두 가지 기준과 비교합니다.

(1) 정직한 광업 전략. 이것은 메인 체인의 주요 블록 만 확장하는 전략입니다.

(2) 단일 트리 이기적인 광업 공격. 이것은 제안 된 비트 코인의 고전적인 이기적인 광업 공격을 정확히 따르는 공격 전략입니다. [11]그러나 개인 체인이 아닌 개인 트리 포크가 자랍니다. 유사하게 [11]대적은 메인 체인의 길이가 개인 나무의 깊이를 따라 잡을 때마다 개인 나무를 출판합니다. 공간 제한으로 인해이 기준의 공식 모델을 생략합니다. 우리는 또한이 기준선을 사용하여 섹션 3.4에서 논의 된 두 번째 제한이 얼마나 심각한 지에 대한 경험적으로 평가합니다.

실험 설정. 우리는 적대적 상대 자원의 값에 대한 우리의 공격과 두 기준선의 실험적 비교를 수행합니다 𝑝 ∈ [0, 0.3] (0.01의 증분) 및 스위칭 확률 𝛾 ∈ {0, 0.25, 0.5, 0.75, 1}. 각 이기적인 광업 공격의 매개 변수에 관해서는 :

• 이기적인 광업 공격의 경우, 우리는 개인 포크의 최대 길이를 설정하고 모든 조합 (𝑑, 𝑓) ∈ {(1, 1), (2, 1), (2, 2), (3, 2), (4, 2)}를 고려합니다.

• 단일 트리 이기적인 광업 공격 기준선의 경우, 개인 트리의 최대 깊이 𝑙 = 4를 최대 개인 포크 길이와 개인 트리의 최대 너비 𝑓 = 5와 일치하도록 설정했습니다.

모든 실험은 Ubuntu 20, 2.80GHz 11 Gen Intel (R) 코어 (TM) i7-1165G7 CPU, 16GB RAM 및 16GB 스왑 SSD 메모리에서 실행되었습니다. 평균 결제 MDP를 해결하기 위해 확률 론적 모델 체커 스톰을 사용합니다. [18]공식 방법 커뮤니티 내에서 인기있는 MDP 분석 도구[2].

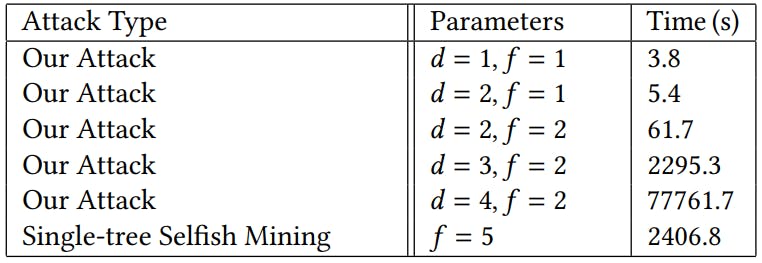
결과. 표 1은 다양한 매개 변수 설정과 𝛾 = 0.5의 고정 스위칭 매개 변수에 대한 단일 트리 이기적인 마이닝 공격뿐만 아니라 이기적인 광업 공격의 런타임을 보여줍니다. 실험의 런타임이 모든 𝛾 매개 변수 설정에서 매우 유사하다는 것을 알았을 때 tim = 0.5에 대한 타이밍 만 표시합니다. 표 1에서 알 수 있듯이, 공격의 깊이를 증가 시키면 상태 공간의 지수 증가로 인해 평가의 런타임이 크게 증가합니다.

실험 결과는 그림 2에 나와 있으며, 각각의 𝛾 ∈ {0, 0.25, 0.5, 0.75, 1}에 대한 플롯을 보여줍니다. 음모에서 볼 수 있듯이, 우리의 이기적인 광업 공격은 일관되게 달성합니다. 예상되는 상대 수익이 높아집니다 𝑑 = 1 및 𝑓 = 1 일 때를 제외하고는 각각의 각 값에 대한 두 기준선보다 errev. 이것은 두 개의 다른 블록에서 개인 포크를 재배하는 것이 이미 단일 블록에서 훨씬 더 큰 개인 트리를 재배하는 것보다 더 강력한 공격을 제공한다는 것을 보여줍니다. 따라서, 우리의 결과는 나무가 아닌 분리 된 개인 포크를 키우는 것이 중요한 제한이 아니며, 분석을 계산적으로 트랙 할 수 있도록 개인 포크를 키우기위한 우리의 선택을 정당화한다는 것을 나타냅니다.

달성 된 Errev는 우리가 𝑑와 𝑓를 증가시키고 대적이 더 비공개 포크를 키울 수있게함으로써 크게 자랍니다. 특히, 𝑑 = 4, 𝑓 = 2 및 상대 적대적 자원 𝑝 = 0.3의 경우, 우리의 공격은 스위칭 확률의 모든 값에 대해 두 기준선의 모든 값보다 0.2 이상의 ERREV를 달성합니다. 이것은 a를 나타냅니다 중요한 이점 효율적인 교정 시스템 블록 체인에서의 이기적인 광업 공격 중 POW와 비교하여 여러 블록에서 여러 개인 포크를 동시에 성장시키는 능력이 훨씬 더 큰 ERREV로 해석되기 때문입니다. 우리의 결과 효율적인 교정 시스템 블록 체인에 대한 합리적인 체인 품질을 유지하기 위해서는 여러 블록의 채굴 할 때 적의 이점을 줄이기위한 기술에 대한 추가 연구가 중요하다는 것을 시사합니다.

마지막으로, 우리는 더 큰 notice 값이 전략에서 더 큰 errev에 해당한다는 것을 알 수 있습니다. 이는 대적 사슬이 메인 체인이 될 가능성에서 더 큰 값이 바이어스를 도입함에 따라 예상된다. 이것은 𝑑 = 𝑓 = 1의 경우에 가장 적절하게 관찰됩니다. 우리가 플롯에서 볼 수 있듯이 𝛾 0.5 및 자원의 비율 𝑝> 0.25에 대해. 모두, 이것은 방송 네트워크에 대한 적의 제어에 대한 더욱 신중하고 신중한 분석과 포크 선택 파괴 규칙이 필요하다는 것을 시사합니다.

주요 테이크 아웃. 실험 평가의 주요 테이크 아웃은 다음과 같습니다.

• 우리의 이기적인 광업 공격이 달성됩니다 상당히 높습니다 Errev는 두 기준선보다 Errev에서 최대 0.2 차이에 도달합니다. 따라서, 우리의 결과는 여러 블록에서 개인 포크를 재배하는 것이 메인 체인의 첫 번째 블록에서 모든 포크를 키우는 것보다 훨씬 유리하다는 것을 강력하게 시사합니다.

• 우리의 결과는 개인 포크가 분리되지 않고 개인 나무를 재배한다고해서 적의 Errev가 크게 개선되지 않을 것이라고 제안합니다. 따라서 섹션 3.4에서 논의 된 우리의 공격의 두 번째 제한은 중요하지 않은 것 같습니다.

• 우리의 결과 효율적인 증거 시스템 블록 체인에서 이기적인 광업 공격에 대한 보안을 향상 시키려면 적의 방송 시스템에 대한 통제를 더욱 신중하게 분석해야한다고 제안합니다. 특히, 스위칭 확률의 큰 값의 경우 𝛾 = 1 및 𝑓 = 1 인 공격의 가장 간단한 변형조차도 𝑝> 0.25 일 때 상환하기 시작합니다.

[2] 구현 세부 정보는 Github 저장소를 참조하십시오.